【Leetcode】【python】Sqrt(x) x 的平方根

题目大意

求一个数的平方根。结果返回整数，舍去小数，不是四舍五入

解题思路

二分搜索：值得注意的是右边可以直接设置为j=x/2+1，因为在(x/2+1)^2 > x。

代码

二分查找

如果不是正好，会左右指针相遇结束循环

class Solution(object):
    def mySqrt(self, x):
        """
        :type x: int
        :rtype: int
        """
        if x == 0:
            return 0
        left = 1
        right = x / 2 + 1

        while left <= right:
            mid = left + (right - left) / 2
            sq = x / mid
            if sq > mid:
                left = mid + 1
            elif sq < mid:
                right = mid - 1
            else:
                return mid
        return right

牛顿法

牛顿迭代法：看到的一种解法
https://shenjie1993.gitbooks.io/leetcode-python/069%20Sqrt.html

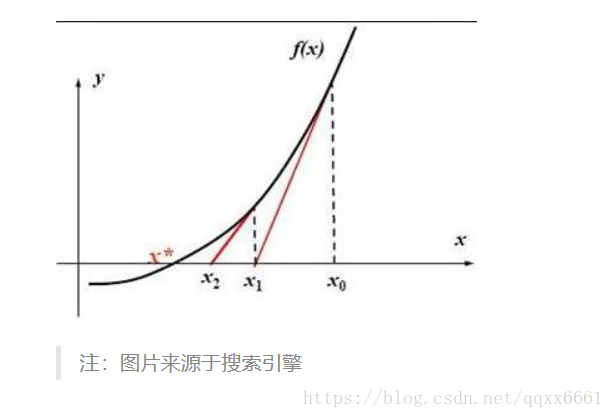
采用牛顿迭代法，通过逼近来求方程 $$y=x^2+a$$ 的解。接单介绍一下牛顿迭代法，如下图，求方程曲线与y轴的交点就是方程的解。随意取一个值 $$X0$$ ，找出曲线在 $$X$$ 处的切线，该切线与y轴的交点为 $$X1$$ ，再求 $$X1$$ 处的切线的交点，可以看出来交点会不断的向目标值靠近，现在确定一个阈值就可以找出近似解了。由于平方根是正数，所以初始的取值应为一个正数。

class Solution(object):
    def mySqrt(self, x):
        """
        :type x: int
        :rtype: int
        """
        result = 1.0
        while abs(result * result - x) > 0.1:
            result = (result + x / result) / 2
        return int(result)


if __name__ == "__main__":
    assert Solution().mySqrt(5) == 2
    assert Solution().mySqrt(0) == 0

我的输入
7
我的标准输出 
result + x , result
8.0 1.0
11.0 4.0
9.875 2.875
我的答案
2

总结