前言

本文总结了常用的全部排序算法，内容包括：

排序算法的定义和思路，动画演示
排序算法的代码实现：Python和Java，包括实现中需要注意的细节
排序算法性能分析：时间空间复杂度分析，稳定排序算法背诵口诀等
不同排序算法最佳使用场景

此文干货颇多，烦请收藏后慢慢研读。

面试知识点复习手册

此文属于知识点复习手册专栏内容，你还可以通过以下两种途径查看全复习手册文章导航：

关注我的公众号：Rude3Knife 点击公众号下方：技术推文——面试冲刺
全复习手册文章导航(CSDN)

—–正文开始—–

算法性能分析

图中纠正：归并排序空间复杂度应该是O(n)，快排是O(logn)-O(n)

稳定性定义：

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

例如，对于如下冒泡排序算法，原本是稳定的排序算法，如果将记录交换的条件改成r[j]>=r[j+1]，则两个相等的记录就会交换位置，从而变成不稳定的算法。

再如，快速排序原本是不稳定的排序方法，但若待排序记录中只有一组具有相同关键码的记录，而选择的轴值恰好是这组相同关键码中的一个，此时的快速排序就是稳定的。

只需记住一句话（快些选一堆美女一起玩儿）是不稳定的，其他都是稳定的。

补充性能图：

不同情况下的合适排序方法

初始数据越无序，快速排序越好。

已经基本有序时，用直接插入排序最快。

在随机情况下，快速排序是最佳选择。

既要节省空间，又要有较快的排序速度，堆排序是最佳选择，其不足之处是建堆时需要消耗较多时间。

若希望排序是稳定的，且有较快的排序速度，则可选用2路归并排序，其缺点需要较大的辅助空间分配。

算法实现

基于比较的排序算法

冒泡排序

思路：

冒泡排序的原理非常简单，它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。

步骤：

比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对第0个到第n-1个数据做同样的工作。这时，最大的数就“浮”到了数组最后的位置上。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

Python:

def bubble_sort(array):
    n = len(array)
    for i in range(n):  # i从0到n
        for j in range(1, n-i):  # 1开始，即j-1=0开始
            if array[j-1] > array[j]:
                array[j-1], array[j] = array[j], array[j-1]
    return array
#优化1：某一趟遍历如果没有数据交换，则说明已经排好序了，因此不用再进行迭代了。
#用一个标记记录这个状态即可。
def bubble_sort2(ary):
    n = len(ary)
    for i in range(n):
        flag = 1                    #标记
        for j in range(1,n-i):
            if  ary[j-1] > ary[j] :
                ary[j-1],ary[j] = ary[j],ary[j-1]
                flag = 0
        if flag :                   #全排好序了，直接跳出
            break
    return ary
#优化2：记录某次遍历时最后发生数据交换的位置，这个位置之后的数据显然已经有序了。
# 因此通过记录最后发生数据交换的位置就可以确定下次循环的范围了。
def bubble_sort3(ary):
    n = len(ary)
    k = n                           #k为循环的范围，初始值n
    for i in range(n):
        flag = 1
        for j in range(1,k):        #只遍历到最后交换的位置即可
            if  ary[j-1] > ary[j] :
                ary[j-1],ary[j] = ary[j],ary[j-1]
                k = j               #记录最后交换的位置
                flag = 0
        if flag :
            break
    return ary

Java:

public void bubble_sort(int [] a) {
        int n = a.length;
        for(int i=0;i<n;i++) {
            for(int j=1;j<n-i;j++) {
                if (a[j-1] > a[j]) {
                    int temp = a[j-1];
                    a[j-1] = a[j];
                    a[j] = temp;
                }
            }
        }
    }
//两种优化不写了

选择排序

思路：

选择排序无疑是最简单直观的排序。它的工作原理如下。

步骤：

在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
以此类推，直到所有元素均排序完毕。

Python:

def selection_sort(array):
    n = len(array)
    for i in range(n):
        minIndex = i
        for j in range(i+1, n):
            if array[j] < array[minIndex]:
                minIndex = j
        array[i], array[minIndex] = array[minIndex], array[i]
# 或者使用minNum存储数值,避免每次都读array[minIndex]，但如果每次都存储新的minNum，也会有损耗。
def selection_sort(array):
    n = len(array)
    for i in range(n):
        minNum = array[i]
        minIndex = i
        for j in range(i+1, n):
            if array[j] < minNum:
                minIndex = j
                minNum = array[j]
        array[i], array[minIndex] = array[minIndex], array[i]

Java：

public void selection_sort(int [] a) {
        int n = a.length;
        for(int i=0;i<n;i++) {
            int minIndex = i;
            for(int j=i;j<n;j++) {
                if (a[j] < a[minIndex]) {
                    minIndex = j;
                }
            }
            int temp = a[i];
            a[i] = a[minIndex];
            a[minIndex] = temp;  
        }
    }

插入排序

思路：

从左边第二个数开始，往前遍历，将大于他的数都往后一个个移位，一旦发现小于等于他的数，就放在那个位置（之前的数已经被移到后面一位了）

插入排序的工作原理是，对于每个未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

步骤：

从第一个元素开始，该元素可以认为已经被排序
取出下一个元素，在已经排序的元素序列中从后向前扫描
如果被扫描的元素（已排序）大于新元素，将该元素后移一位
重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
将新元素插入到该位置后
重复步骤2~5

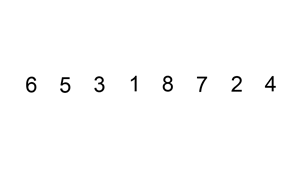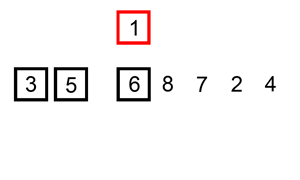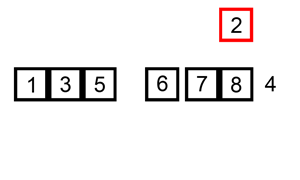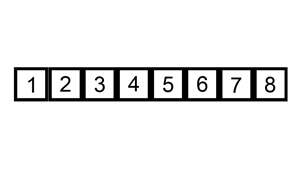
Python：

def insert_sort(array):
    n = len(array)
    for i in range(1,n): # 从第二个数开始
        if array[i-1] > array[i]:  # 前面比后面大，需要调整位置
            num = array[i]
            index = i
            for j in range(i-1, -1, -1):
                if array[j] > num:
                    array[j+1] = array[j]
                    index = j
                else:  # 找到位置，插入
                    array[index] = num
                    break

Java：

public void insert_sort(int [] a) {
        int n = a.length;
        for(int i=1;i<n;i++) {
            if (a[i-1] > a[i]) {
                int num = a[i];
                int index = i;
                for(int j=i-1;j>-1;j--) {
                if (a[j] > num) {
                    a[j+1] = a[j];
                    index = j;
                }
                else {
                    a[index] = num;
                    break;
                }
                }
            } 
        }
    }

希尔排序（递减增量排序算法，实质是分组插入排序）

思路：

希尔排序的基本思想是：将数组列在一个表中并对列分别进行插入排序，重复这过程，不过每次用更长的列（步长更长了，列数更少了）来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法，算法本身还是使用数组进行排序。

例如，假设有这样一组数，

1	[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]

如果我们以步长为5开始进行排序，我们可以通过将这列表放在有5列的表中来更好地描述算法，这样他们就应该看起来是这样：

13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10

然后我们对每列进行排序：

10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45

将上述四行数字，依序接在一起时我们得到：

1	[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ]

。这时10已经移至正确位置了，然后再以3为步长进行排序：

排序之后变为：

最后以1步长进行排序（此时就是简单的插入排序了）。

具体实现：外面套一个gap，while内做插入排序，并且将gap不断除2，直到小于0出循环

Python：

def shell_sort(ary):
    n = len(ary)
    gap = round(n/2)  # 初始步长 , 用round取整(注意0.5向下取)
    while gap > 0 :
        for i in range(gap,n):  # 每一列进行插入排序 , 从gap 到 n-1
            temp = ary[i]
            index = i
            while ( index >= gap and ary[index-gap] > temp ):  # 插入排序
                ary[index] = ary[index-gap]
                index = index - gap
            ary[index] = temp
        gap = round(gap/2)  # 重新设置步长
    return ary

Java：

public void shell_sort(int [] a) {
        int n = a.length;
        int gap = n / 2;
        while (gap > 0) {
            for (int i=gap;i<n;i++) {
                int temp = a[i];
                int j = i;
                while (j>=gap && a[j-gap] > temp) {
                    a[j] = a[j-gap];
                    j = j - gap; 
                    }
                a[j] = temp;
            }
        gap = gap / 2;
        }
    }

归并排序(递归合并)

思路：拆拆拆到单个数字，合并合并合并

归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组，再合并数组。

先考虑合并两个有序数组，基本思路是比较两个数组的最前面的数，谁小就先取谁，取了后相应的指针就往后移一位。然后再比较，直至一个数组为空，最后把另一个数组的剩余部分复制过来即可。

再考虑递归分解，基本思路是将数组分解成left和right，如果这两个数组内部数据是有序的，那么就可以用上面合并数组的方法将这两个数组合并排序。如何让这两个数组内部是有序的？可以再二分，直至分解出的小组只含有一个元素时为止，此时认为该小组内部已有序。然后合并排序相邻二个小组即可。

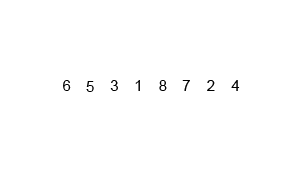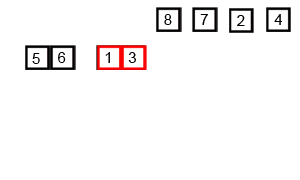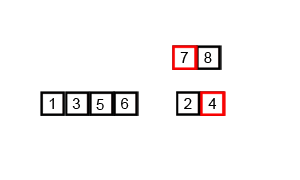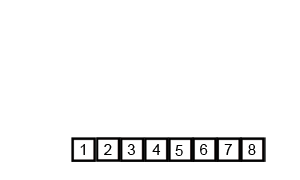
Python：

def merge_sort(array):  # 递归
    if len(array) <= 1: return array  # python每次都是新的数组，可以用数组长度小于等于1来判断
    num = len(array) // 2  # py27 3/2和3//2相同,python3 3//2才是地板除
    left = merge_sort(array[:num])
    right = merge_sort(array[num:])
    return merge(left, right)

def merge(left, right):  # 合并
    l,r = 0,0
    result = []
    while l < len(left) and r < len(right):
        if left[l] < right[r]:
            result.append(left[l])
            l = l + 1
        else:
            result.append(right[r])
            r += 1
    # 一边没有之后，加上所有的
    result += left[l:]
    result += right[r:]
    return result

Java：

//注意：新建的temp长度和原数组是一样的，所以额外空间是O（n），temp数组一开始并未赋值，在合并时慢慢给其填充数值，所以说一共只有一个temp数组
public void mergeSort(int[] arr) {
        mergeSort(arr, new int[arr.length], 0, arr.length - 1);
    }

    private static void mergeSort(int[] arr, int[] temp, int left, int right) {
        if (left < right) {  // Java则通过左右指针来判断
            int center = (left + right) / 2;
            mergeSort(arr, temp, left, center); // 左边
            mergeSort(arr, temp, center + 1, right); // 右边
            merge(arr, temp, left, center + 1, right); // 合并两个有序
        }
    }
    private static void merge(int[] arr, int[] temp, int leftPos, int rightPos, int rightEnd) {
        int leftEnd = rightPos - 1; // 左边结束下标
        int tempPos = leftPos; // 从左边开始算
        int numEle = rightEnd - leftPos + 1; // 元素个数
        while (leftPos <= leftEnd && rightPos <= rightEnd) {
            if (arr[leftPos] <= arr[rightPos])
                temp[tempPos++] = arr[leftPos++];
            else
                temp[tempPos++] = arr[rightPos++];
        }
        while (leftPos <= leftEnd) {  // 左边如果有剩余
            temp[tempPos++] = arr[leftPos++];
        }
        while (rightPos <= rightEnd) { // 右边如果有剩余
            temp[tempPos++] = arr[rightPos++];
        }
        // 将temp复制到arr，覆盖原来这里的位置
        for (int i = 0; i < numEle; i++) {
            arr[rightEnd] = temp[rightEnd];
            rightEnd--;
        }
    }

快速排序

快速排序通常明显比同为Ο(n log n)的其他算法更快，因此常被采用，而且快排采用了分治法的思想，所以在很多笔试面试中能经常看到快排的影子。可见掌握快排的重要性。

快排特点：

每经过一趟快排，轴点元素都必然就位，也就是说，一趟下来至少有关键字key节点在其最终位置，所以考察各个选项，看有几个元素就位即可。
逆序的数列，选择首位为key，则会退化到O（n^2），可以随机选择一个元素作为基准元素。

两种交换方法：

指针交换法：youtube视频：https://www.youtube.com/watch?v=gl_XQHTJ5hY （下图代码实现的方法，并且是两两交换，最后将key与left交换）

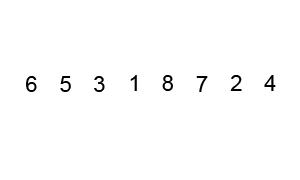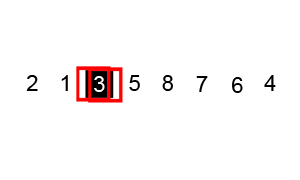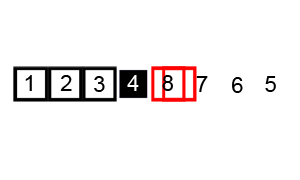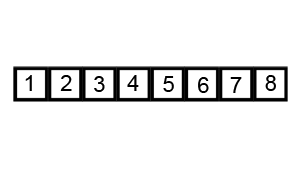
挖坑填数法：http://blog.csdn.net/morewindows/article/details/6684558 （key一开始就被挖坑填写了别的数，我认为第二种是做牛客网选择题时需要掌握的，应为选择题答案的排序结果通常是按照这种算法得到的排序结果）

快排优化方法：

https://blog.csdn.net/cpcpcp123/article/details/52739285

选择基准的方式：三数取中（median-of-three）

举例：待排序序列为：8 1 4 9 6 3 5 2 7 0

左边为：8，右边为0，中间为6.

我们这里取三个数排序后，中间那个数作为枢轴，则枢轴为6

下图分别对应第一种和第二种排序的中间结果：

Python(指针交换)：

def quick_sort(ary):
    return _quick_sort(ary, 0, len(ary)-1)
def _quick_sort(ary, left, right):
    if left >= right: return ary
    key = ary[left]  # 每次都选最左边为key
    lp = left
    rp = right
    while (lp < rp):
        while ary[rp] >= key and lp < rp:
            rp -= 1
        while ary[lp] <= key and lp < rp:
            lp += 1
        ary[lp], ary[rp] = ary[rp], ary[lp]
    ary[left], ary[lp] = ary[lp], ary[left]  # 这里不能用key，是交换数组内数字
    _quick_sort(ary, left, lp-1)
    _quick_sort(ary, lp+1, right)  # 这里lp, rp永远是相等的。所以都可以。
    return ary

Java(指针交换)：

public void quick_sort(int[] ary) {
        _quick_sort(ary, 0, ary.length-1);
    }
    public void _quick_sort(int[] ary, int left, int right) {
        if (left < right) { 
            int key = ary[left];
            int lp = left;
            int rp = right;
            while (lp < rp) {
                while (ary[rp] >= key && lp < rp ) {
                    rp--;
                }
                while (ary[lp] <= key && lp < rp ) {
                    lp++;
                }
                int temp = ary[lp];
                ary[lp] = ary[rp];
                ary[rp] = temp;
            }
            int temp = ary[lp];
            ary[lp] = ary[left];
            ary[left] = temp;
            _quick_sort(ary, left, lp-1);
            _quick_sort(ary, rp+1, right);
        }
    }

Java(挖坑法)

非递归形式实现（栈）：和刚才的递归实现相比，代码的变动仅仅在quickSort方法当中。该方法中引入了一个存储Map类型元素的栈，用于存储每一次交换时的起始下标和结束下标。

每一次循环，都会让栈顶元素出栈，进行排序，并且按照基准元素的位置分成左右两部分，左右两部分再分别入栈。当栈为空时，说明排序已经完毕，退出循环。

该方法实现代码请参考程序员小灰：

https://mp.weixin.qq.com/s?__biz=MzIxMjE5MTE1Nw==&mid=2653195042&idx=1&sn=2b0915cd2298be9f2163cc90a3d464da&chksm=8c99f9f8bbee70eef627d0f5e5b80a604221abb3a1b5617b397fa178582dcb063c9fb6f904b3&mpshare=1&scene=1&srcid=0813k35KHoSO42jGGrMx5oUA#rd

堆排序

参考：

http://blog.csdn.net/minxihou/article/details/51850001

https://www.2cto.com/kf/201609/549335.html

例题：相当帮助理解

https://www.nowcoder.com/test/question/done?tid=14276624&qid=56294#summary

思路：

父节点i的左子节点在位置(2*i+1)

父节点i的右子节点在位置(2*i+2)

子节点i的父节点在位置floor((i-1)/2)

堆排序构建堆的时间复杂度是N,而重调堆的时间复杂度是logN

堆可以分为大根堆和小根堆，这里用最大堆的情况来定义操作:

(1)最大堆调整(MAX_Heapify):

将堆的末端子节点作调整，使得子节点永远小于父节点。这是核心步骤，在建堆和堆排序都会用到。比较i的根节点和与其所对应i的孩子节点的值。当i根节点的值比左孩子节点的值要小的时候，就把i根节点和左孩子节点所对应的值交换，当i根节点的值比右孩子的节点所对应的值要小的时候，就把i根节点和右孩子节点所对应的值交换。然后再调用堆调整这个过程，可见这是一个递归的过程。

(2)建立最大堆(Build_Max_Heap):

将堆所有数据重新排序。建堆的过程其实就是不断做最大堆调整的过程，从len/2出开始调整，一直比到第一个节点。

(3)堆排序(HeapSort):

移除位在第一个数据的根节点，并做最大堆调整的递归运算。堆排序是利用建堆和堆调整来进行的。首先先建堆，然后将堆的根节点选出与最后一个节点进行交换，然后将前面len-1个节点继续做堆调整的过程。直到将所有的节点取出，对于n个数我们只需要做n-1次操作。堆是用顺序表存储的的代码可以先看：http://blog.51cto.com/ahalei/1427156 就能理解代码中的操作

注意：

从小到大排序的时候不建立最小堆而建立最大堆。最大堆建立好后，最大的元素在h[ 1]。因为我们的需求是从小到大排序，希望最大的放在最后。因此我们将h[ 1]和h[ n]交换，此时h[ n]就是数组中的最大的元素。

请注意，交换后还需将h[1]向下调整以保持堆的特性。OK现在最大的元素已经归位，需要将堆的大小减1即n–，然后再将h[1]和h[ n]交换，并将h[1]向下调整。如此反复，直到堆的大小变成1为止。此时数组h中的数就已经是排序好的了。

代码如下：

Python:

def MAX_Heapify(heap, HeapSize, root):  # 在堆中做结构调整使得父节点的值大于子节点

    left = 2 * root + 1
    right = left + 1
    larger = root
    if left < HeapSize and heap[larger] < heap[left]:
        larger = left
    if right < HeapSize and heap[larger] < heap[right]:  # 确定到底和左还是右节点换，先判断做节点
        larger = right
    if larger != root:  # 如果做了堆调整：则larger的值等于左节点或者右节点的，这个时候做对调值操作
        heap[larger],heap[root] = heap[root],heap[larger]
        MAX_Heapify(heap, HeapSize, larger)  # 从顶端递归往下调整，用larger是因为larger是数组索引，并且已经在比较时候更新过，而root没有更新过！

def Build_MAX_Heap(heap):  # 构造一个堆，将堆中所有数据重新排序
    HeapSize = len(heap)
    for i in range(((HeapSize-1）-1)//2,-1,-1):  # 从后往前出数(z最后一个节点的父节点)  '//' got integer
        MAX_Heapify(heap,HeapSize,i)  # 这里堆的大小是固定，root是i逐步减小

def HeapSort(heap):  # 将根节点取出与最后一位做对调，对前面len-1个节点继续进行对调整过程。
    Build_MAX_Heap(heap)
    for i in range(len(heap)-1,-1,-1):
        heap[0],heap[i] = heap[i],heap[0]
        MAX_Heapify(heap, i, 0)  # 这里堆的大小是逐步缩小，root永远是0
    return heap

Java：

有空补

非基于比较的排序算法

基于比较的排序算法是不能突破O(NlogN)的。简单证明如下：

N个数有N!个可能的排列情况，也就是说基于比较的排序算法的判定树有N!个叶子结点，比较次数至少为log(N!)=O(NlogN)(斯特林公式)。

计数排序

计数排序在输入n个0到k之间的整数时(可以从a到b，不用非要从0开始，代码可以实现)，

时间复杂度最好情况下为O(n+k),最坏情况下为O(n+k),平均情况为O(n+k),空间复杂度为O(n+k)

算法的步骤如下：

1.找出待排序的数组中最大和最小的元素

2.统计数组中每个值为i的元素出现的次数，存入数组C的第i项

3.对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）

4.反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1

当k不是很大时，这是一个很有效的线性排序算法。更重要的是，它是一种稳定排序算法，即排序后的相同值的元素原有的相对位置不会发生改变(表现在Order上)，这是计数排序很重要的一个性质，就是根据这个性质，我们才能把它应用到基数排序。

# -*- coding:utf-8 -*-
def count_sort(ary):
	max=min=0  # min和max应该用sys.maxint
	for i in ary:
		if i < min:
			min = i
		if i > max:
			max = i 
	count = [0] * (max - min +1)
	for index in ary:
		count[index-min]+=1
	index=0
	for a in range(max-min+1):
		for c in range(count[a]):  # 重点：有多少个就for循环多少次
			ary[index]=a+min
			index+=1
	return ary

桶排序

假如待排序列K= {49、 38 、 35、 97 、 76、 73 、 27、 49 }。这些数据全部在1—100之间。因此我们定制10个桶，然后确定映射函数f(k)=k/10。则第一个关键字49将定位到第4个桶中(49/10=4)。依次将所有关键字全部堆入桶中，并在每个非空的桶中进行快速排序。

因此，我们需要尽量做到下面两点：

(1) 映射函数f(k)能够将N个数据平均的分配到M个桶中，这样每个桶就有[N/M]个数据量。

(2) 尽量的增大桶的数量。极限情况下每个桶只能得到一个数据，这样就完全避开了桶内数据的“比较”排序操作。当然，做到这一点很不容易，数据量巨大的情况下，f(k)函数会使得桶集合的数量巨大，空间浪费严重。这就是一个时间代价和空间代价的权衡问题了。

对于N个待排数据，M个桶，平均每个桶[N/M]个数据的桶排序平均时间复杂度为：
O(N)+O(M*(N/M)log(N/M))=O(N+N(logN-logM))=O(N+NlogN-NlogM)
当N=M时，即极限情况下每个桶只有一个数据时。桶排序的最好效率能够达到O(N)。

桶排序是稳定的。

基数排序

基数排序的思想就是将待排数据中的每组关键字依次进行桶分配。比如下面的待排序列：

278、109、063、930、589、184、505、269、008、083

我们将每个数值的个位，十位，百位分成三个关键字： 278 -> k1(个位)=8 ，k2(十位)=7 ，k3=(百位)=2。

然后从最低位个位开始(从最次关键字开始)，对所有数据的k1关键字进行桶分配(因为，每个数字都是 0-9的，因此桶大小为10)，再依次输出桶中的数据得到下面的序列。

930、063、083、184、505、278、008、109、589、269

再对上面的序列接着进行针对k2的桶分配，输出序列为：

505、008、109、930、063、269、278、083、184、589

最后针对k3的桶分配，输出序列为：

008、063、083、109、184、269、278、505、589、930

很明显，基数排序的性能比桶排序要略差。每一次关键字的桶分配都需要O(N)的时间复杂度，而且分配之后得到新的关键字序列又需要O(N)的时间复杂度。假如待排数据可以分为d个关键字，则基数排序的时间复杂度将是O(d*2N) ，当然d要远远小于N，因此基本上还是线性级别的。基数排序的空间复杂度为O(N+M)，其中M为桶的数量。一般来说N>>M，因此额外空间需要大概N个左右。

但是，对比桶排序，基数排序每次需要的桶的数量并不多。而且基数排序几乎不需要任何“比较”操作，而桶排序在桶相对较少的情况下，桶内多个数据必须进行基于比较操作的排序。因此，在实际应用中，基数排序的应用范围更加广泛。